[10000印刷√] 五角形 の 角度 553995-五角形の角度の合計
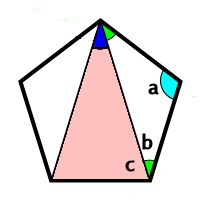
課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を・五角形の場合:n=5 ・内部に作成できる三角形の数:n-2=5-2=3個 540度 どうですか?五角形の内角の和は540度で間違いないですよね? したがって、 となるのです。これが 公式 ですよ^^ 図のように外角を使って考えてもいいし、 対頂角は等しいので、内角から対頂角を除いた角度cd=abと考えてもOK。 この形は単体では問題にあまりでてきませんが、ある図形の一部がこの形という風に出題されます。 この3つの形は角度の問題を解いて
五角形5 辺と対角線の比 Wandering In The Woods
五角形の角度の合計
五角形の角度の合計-第314問 正五角形と角度 図形ドリル 5年生 6年生 new 正五角形 角度 ★★★☆☆☆ (中学入試標準レベル) 思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げてい加法定理や,15°シリーズの三角比以外で求められる三角比として,有名なのが $\cos72^\circ$ や $\cos36^\circ$ などの$18^\circ$ シリーズの三角比です. ベクトルで正五角形の問題などと絡めて出題されたりします.このページは,これらの問題が比較的よく出る大学の志望者向けです.
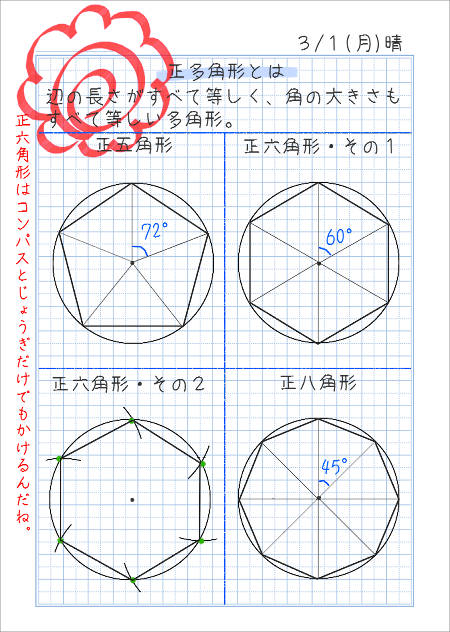



いろいろな正多角形をかいてみよう 家庭学習レシピ
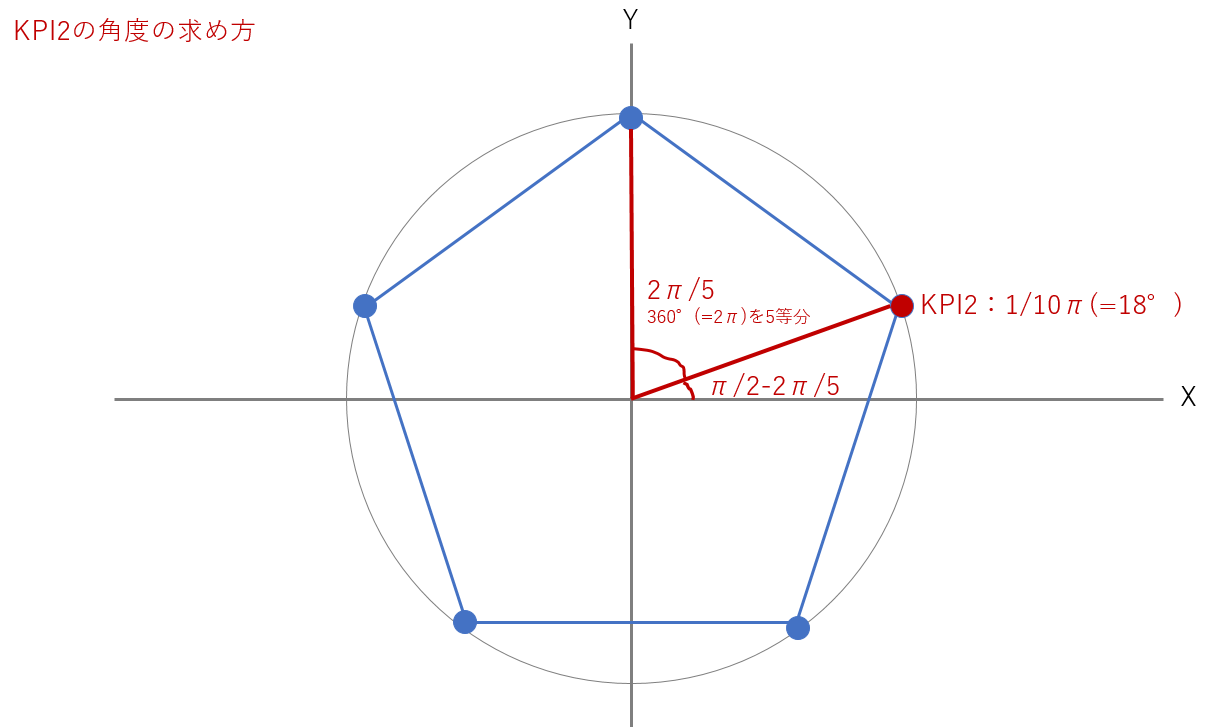
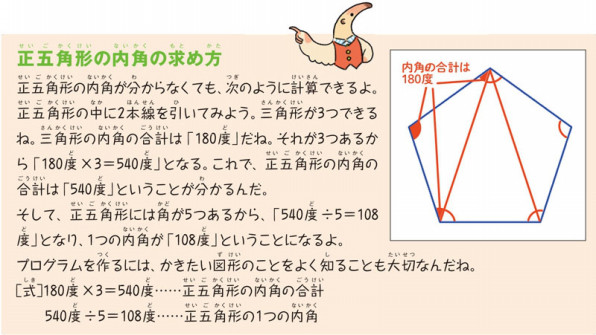
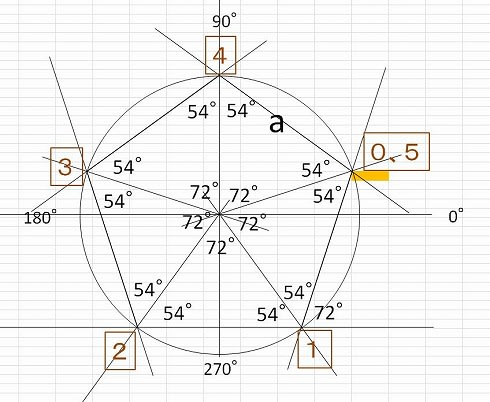
Unknown (Unknown) 1025 もり 様 たとえば、点Aに、5つの辺に平行な線を集めてみますと 点Aを中心に角度が10等分された線が現れます。 辺OC、辺ODの 平行線も引きますと 最初に図形の中に現れる角度の同位角が 点Aの周りにあります。 点Aを中心に角度が10等分された線の真ん中に 五角形の中に三角形が3つも潜んでいるから なんだ。 まず、 対角線を2本ひいてみよう。 すると、どうだろう?? 三角形が3つも隠れていることがわかるよね。 三角形の内角の和は「180°」で、5角形には三角形が3つもかくれているんだ。 よって、 五角形の2-4-1 星型多角形の内角の和 教材(問題場面) 図のように5つの点A,B,C,D, Eがある。
分度器や直線定規を使って正五角形を描く方法です。 数学的には正解ではない作図法です。 ☆用具:直線定規、コンパス、分度器 (1) 点oを中心とした円と、点oを通る直線と、それに直角に交わる垂直線を描く。 (2) 中心の点oから72度の角度に5本の線を引いそして、あなたは正五角形を持っています: 下のマークから折りたたみ、右のマークを上の線に合わせることは、構造に必要な角度を作成することによって、最も重要な部分のようです。 この折り目は私に 折り紙の三等分を思い出させます。 これは近似② 本時の課題を知る 星形五角形の頂角の和は柑00 であることを 確認する 多様な考え方にもふれておく 規則性の追究にもふれておく 「1つの円周上に並んだ5つの点を1 つ飛びで結んでできる星形多角形の頂角 の和を求めてみよう。」という前時の課
三角形の外角 赤色の角度のことを、ぜんぶ 「外角」 と呼ぶよ! 三角形の1辺を延長して外角を理解しよう! 三角形の1つの外角は、その隣にない2つの内角の和と等しい はい。これ意味わかる・・・?クソわかりづらいよね?ウンウン。。 下の図で解説問題に挑戦してみよう! 正多角形の内角・外角 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝に黒い角度の和は,五角 形の内角の和になってい るから,540度。 (星形の角度 基本を参照) 星形の角度を求めるの に便利な公式を利用する と,右の図の白い角度の 和は,黒い角度の和と等 しいことがわかる。 右の図の黒い角度の和 を求めればよい。




スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学
平行線の同位角と錯角を利用して角度を求める問題の解き方の解説です。 分かり易いところなので得点しやすいですが、理解していないと大きな差となります。 落とせないところなのでいくつかの出題パターンを確認しておきましょう。 1ウ 五角形の外角の和を利用する 図のように,星型五角形の5つの角をそれぞれ 頂点とする三角形の角の和から五角形の外角の 和を2つ分ひき,180°と求めることができる。 B ①では,図形の性質を利用することで星型五角形 の内角の和を演繹的に求める例を星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して
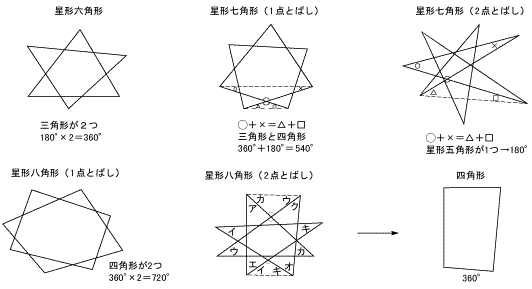



課題学習の指導 数学



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
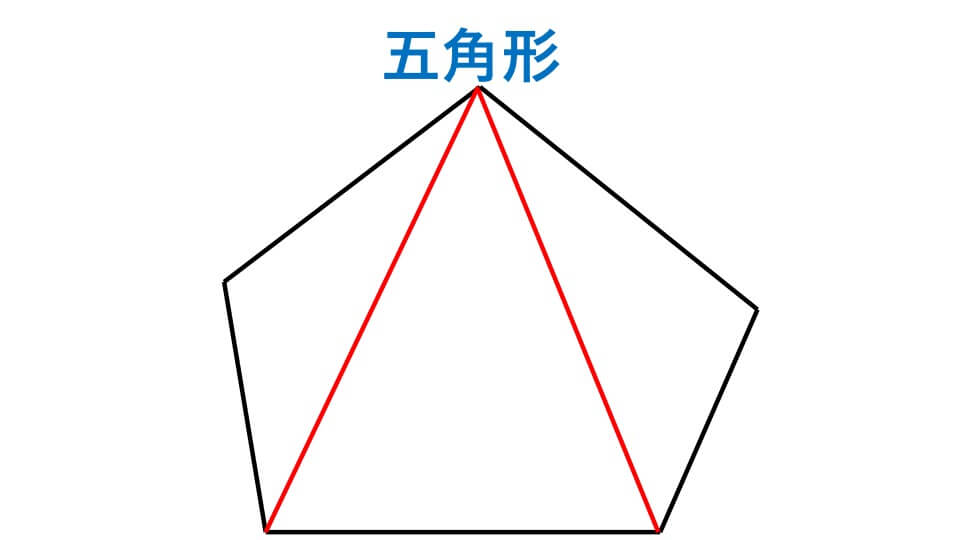
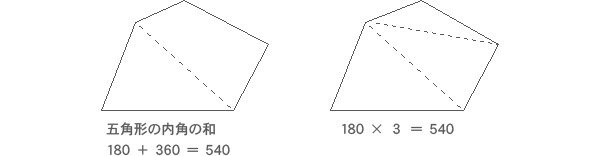
五角形の角度の問題を解いてみましょう。基礎知識多角形の内角と外角 内角: 図1の頂点1、2、3、・・・、n の内側の角。 外角: 図2の∠a、∠b、∠c 、・・・、∠n 。 n 角形の内角の五角形は三角形が3つ 六角形は三角形が4つ ・・・ と増えていくだけです。 なので多角形の内角の和は三角形の数に関係しています。 三角形の内角の和は\(\,180°\,\) これは忘れたら角度は求まりません。 多角形の内角の和の公式を表しておきます。 この五角形は赤線で示したように三角形3つ分に分けることができます。三角形の数は(52=3)で求めることができます。 三角形の内角の和は180°なので、五角形の内角の和は、180°×3=540° になります。 多角形の角の性質を下の表にまとめました。




多角形の内角の和 は何度なのか を説明します おかわりドリル



オリジナル 五角形 の 角度 壁紙 おしゃれ トイレ
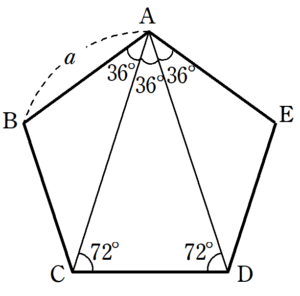
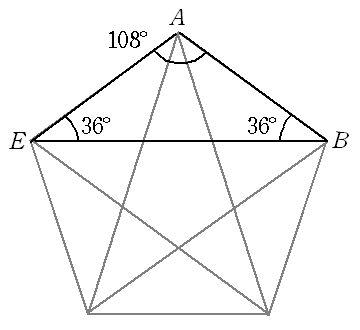
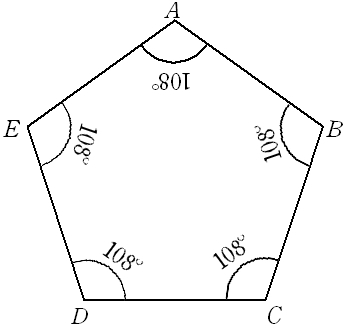
正五角形の性質 正三角形・正方形・正六角形に引き続き、正五角形編です。 相似 まずは角度に注目。 内角の和が540°なので、1つの内角が 108° 。 対角線を引いたら内角が 3等分 されます。 分解してできる三角形の内角は、 36°、72°、108°の3種類 。 そして、 36°72°108°=123 になっています。 この赤線が「五角形」の一辺の長さになります。 コンパスの角度を変えずに、ほかの点にも印をつけていきます。 6五角形を作っていきます。順番に線を引いていくと五角形になります。 10完成です 11次は「星」を作ります。 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、 180°(n2)/ n で計算できちゃうって公式だ。 さっそく、正五角形の内角を計算してみよう! 正五角形は頂点が5つあるから、




課題学習の指導 数学



Tableauでレーダーチャートをつくってみた 応用編 Tabろぐ
どうもみなさん!こんにちは。カズズです。 ホームベースって、わかりますよね。 もちろん、野球とかでキャッチャーやバッターの前にあって、そこをめがけてピッチャーが投げる五角形のやつです。 ストライク・ボールの判定や、得点に絡んだアウト・セーフの判定等ホームベースを問題 (奈良学園登美ヶ丘中学 09年、早稲田中学 10年 女子学院中学 14年 受験問題 算数) 難易度★★★ 1 1辺の長さが等しい正五角形と正六角形を、下の図Ⅰのように1つの辺を重ねました。このとき、アの角度は何度ですか。②n=7のとき、星形七角形の角を求 めよう。 三角形2つ分である→360°だ。 角度を移動させていくと540°だ。 個人思考5分 ↓ 班員で共有・A3用紙にまとめ7分 全体に説明する。 自分の考えをまとめる。 角度とnの関係に、ある法則がな いか考えさせる。




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




発展 円に内接する正五角形の作図 デザインあ おとなスペシャルで紹介されてたやつ なかけんの数学ノート
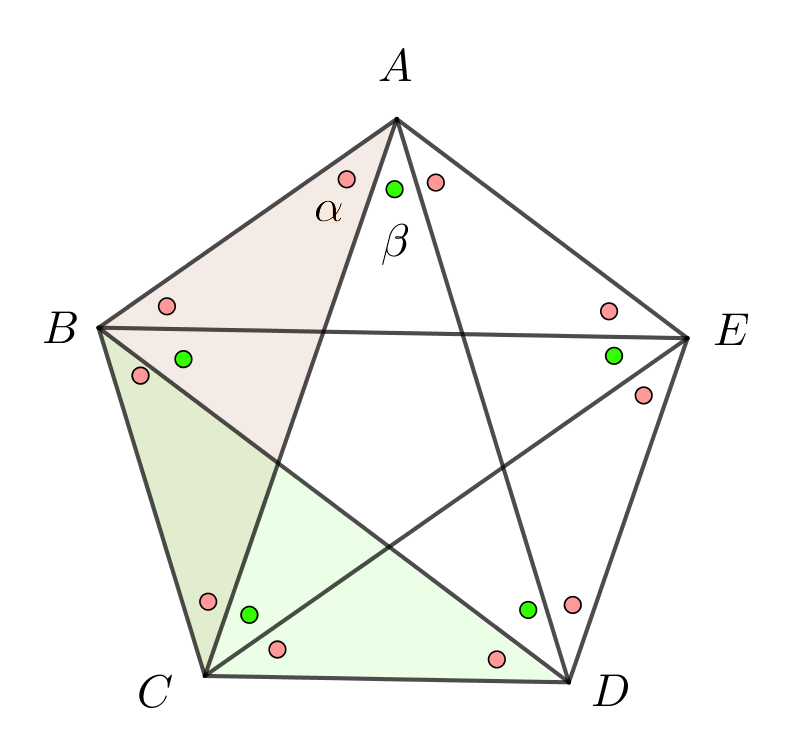
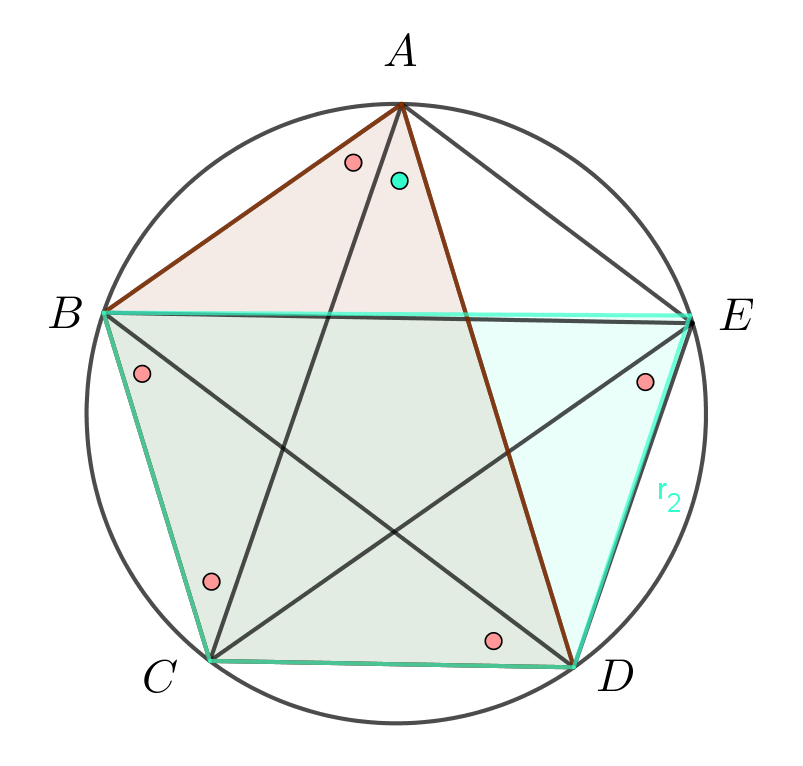
第1時 (1) 本時の学習課題を提示する。 右の図のように5つの点A,B,C,D,Eがある。 これらの点を2つおきに結んでえられる星形五角形の頂角の和 ∠a+∠b+∠c+∠d+∠e について調べてみよう。 (2) 予想させる。 ・頂角の和は何度になると思いますか




黄金三角形による18 シリーズの三角比 おいしい数学



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく




角度の問題 解答編 塾講師 かく語りき



正五角形の中の角度



星形の角度の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



敷き詰めの探究 Part 1 数理女子




多角形の内角の和 算数の公式覚えてますか



Lとmは平行であり 五角形abcdeは正五角形である Xの Yahoo 知恵袋
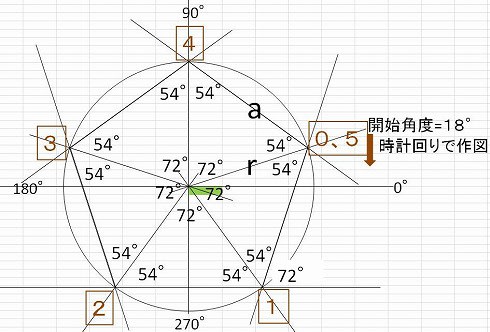



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみました 日だまりのエクセルと蝉しぐれ
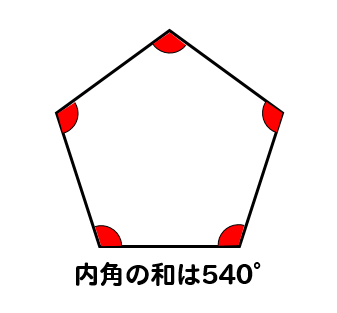



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




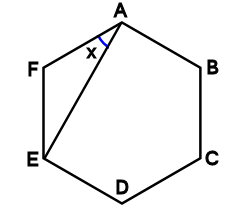
角xの求め方を教えて下さい 答えは17度です Clearnote




小5 算数 小5 54 正多角形 Youtube




いろいろな正多角形をかいてみよう 家庭学習レシピ




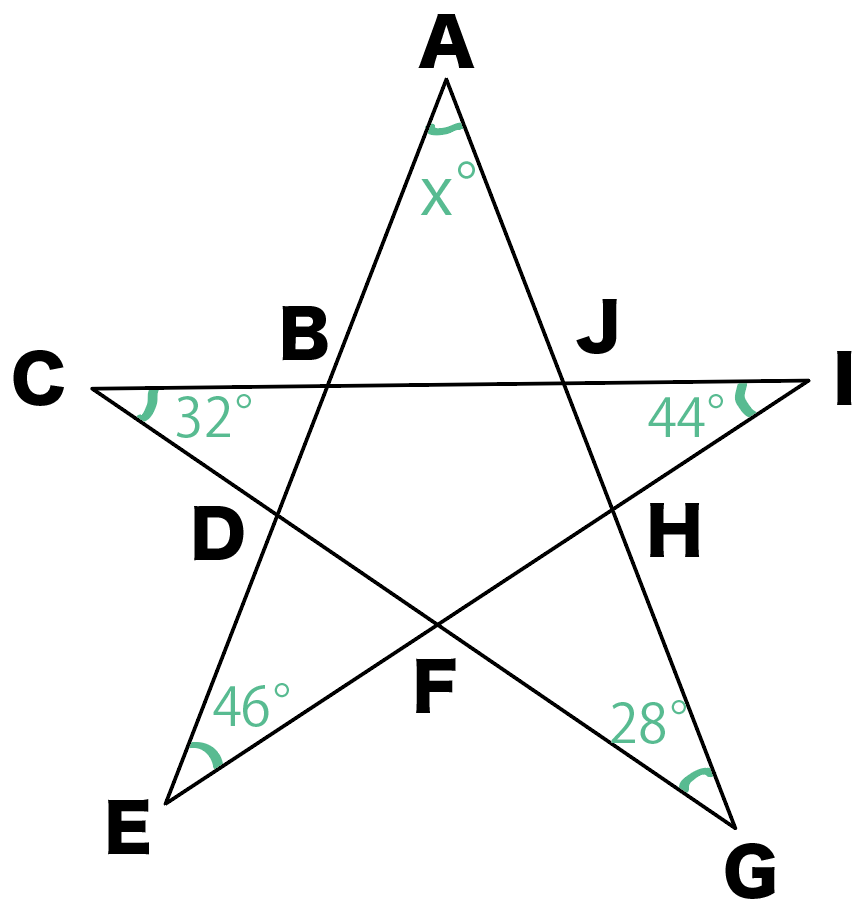
星の五角形の問題です どうやって角度を求めればいいですか Clearnote




中学2年生 覚えておくと便利な角度の関係 公式 個別進学教室マナラボ受験 教育情報サイト




どこで間違えてるか教えて下さい ˊᵕˋ Xの角度を求める問題です Clearnote



平面図形の角度 第81問 正五角形 女子学院中学 入試問題 13年 平成25年度 算数 まいにち一題 中学受験過去問題研究



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか



角度 五角形 中学から数学だいすき




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト
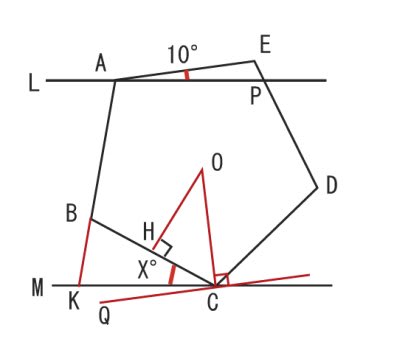



正五角形というだけで 分かる角度は 名寄 算数数学教室より



正五角形 正六角形 の 内角の和 と 一辺の角度は何 か 教 Yahoo 知恵袋
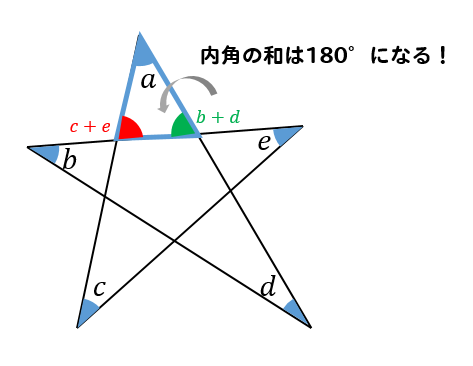



星形の角度 内角の和の求め方を問題解説 数スタ



正五角形



五角形



多角形の内角と外角 思考力を鍛える数学




五角形の5つの角の大きさの和を計算する式 東京大学附属中学校 年 恋する中高一貫校 適性検査 徹底攻略
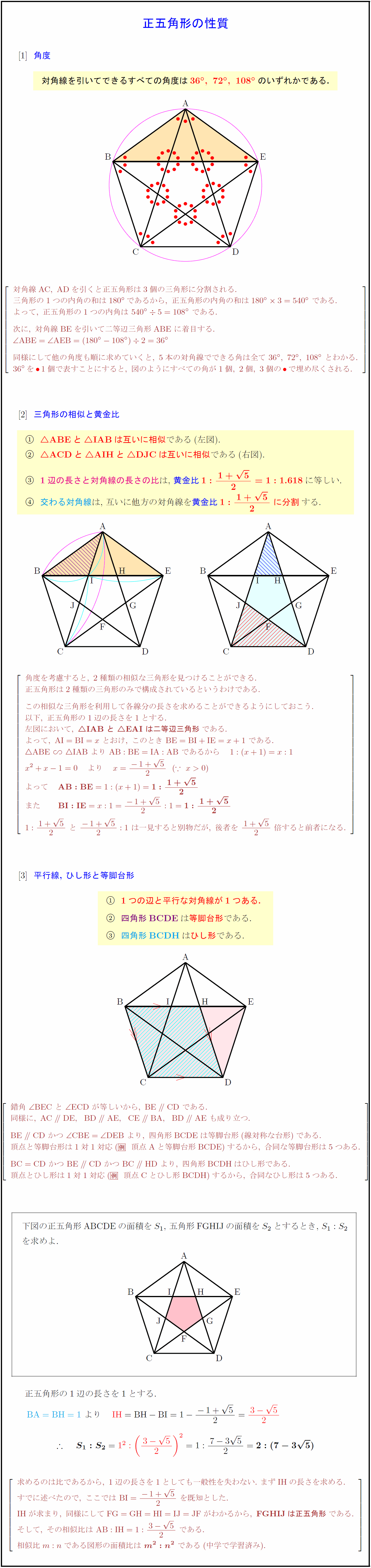



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学



図形 正五角形の分解 父ちゃんが教えたるっ



正五角形を描く ウソの国ー詩と宗教 戸田聡 St5402jp
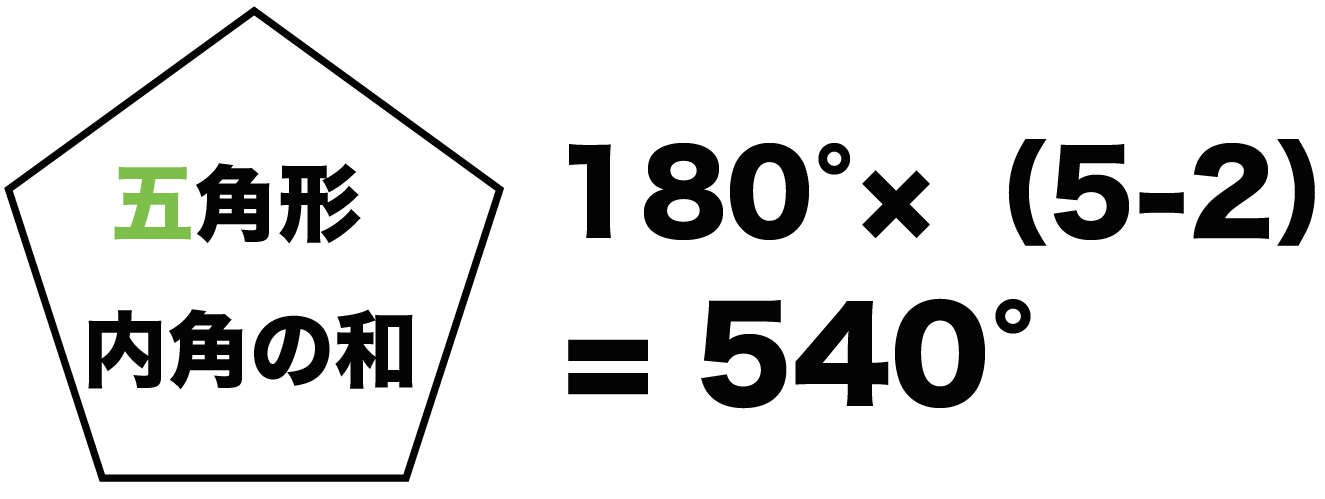



簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく



正多角形の内角と中心角 家紋の描き方007b 夏貸文庫




小5 算数 小5 33 五角形 六角形 多角形 Youtube



南山中学女子部過去問題演習
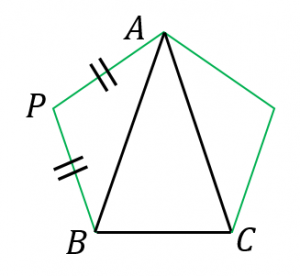



正五角形の対角線の長さと高さ 具体例で学ぶ数学



正五角形です あ い うの角度の求め方教えてください あ36 Yahoo 知恵袋



多角形 の内角の角度 計算ドリル 問題集 数学fun



正五角形




五角形5 辺と対角線の比 Wandering In The Woods



3



正多角形の面積の公式 Fukusukeの数学めも




32面体の面のなす角度 趣味の木工 木工旋盤のホーム ページ



正五角形の中の角度



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



My Math Note




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
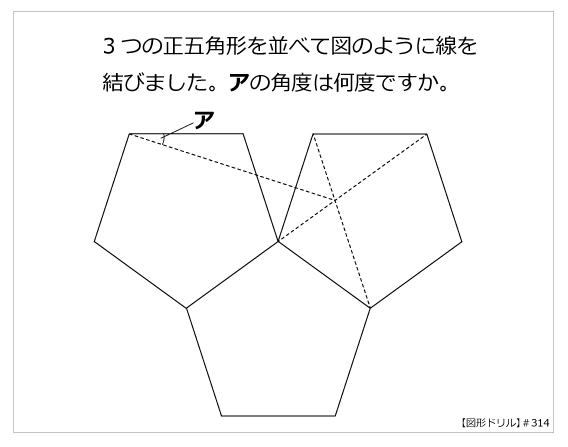



第314問 正五角形と角度 図形ドリル 第314問 正五角形と角度 算数星人のweb問題集 中学受験算数の問題に挑戦




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



早稲田11 2 の 1 角度 正五角形と正三角形が重なった図形 気まぐれ解説カフェ 仮
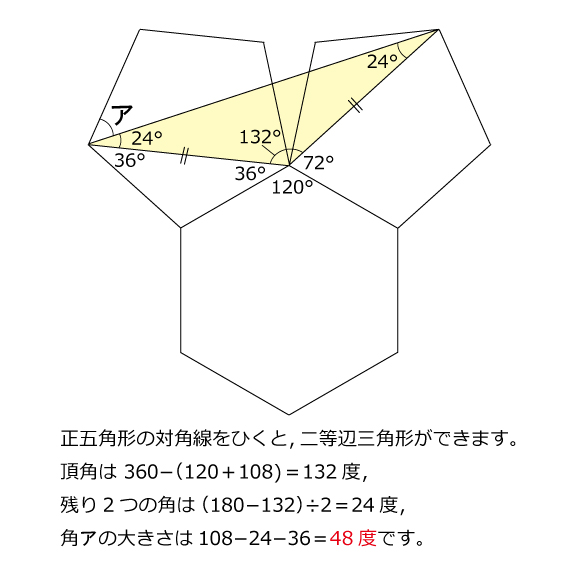



早稲田中 正五角形と正六角形21年早稲田中 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦



正五角形の内角 外角



2




数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
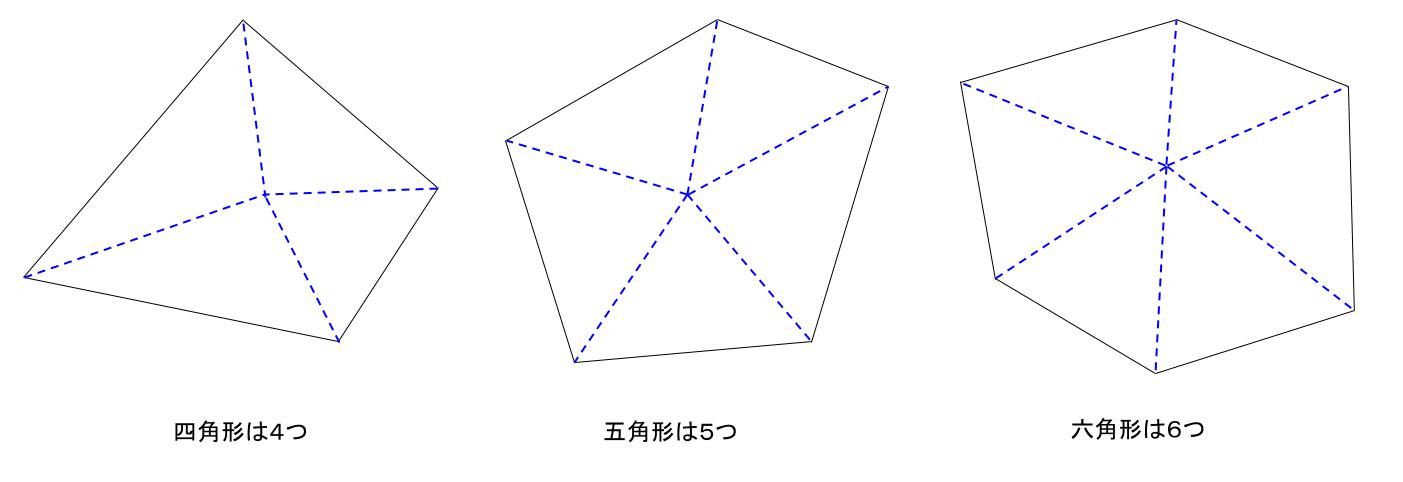



中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su



茗渓予備校 科目情報




数学 中2 53 角度チャレンジ Lv 1 Youtube
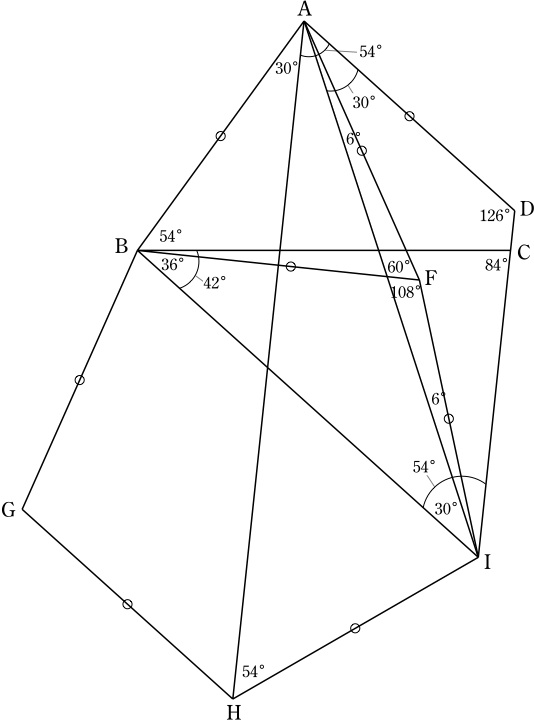



幾何大王からの挑戦状 角度の問題 24 解答例



ちょっと戸惑う角度問題 共立女子中学 2009年 これが中学入試に出た図形問題
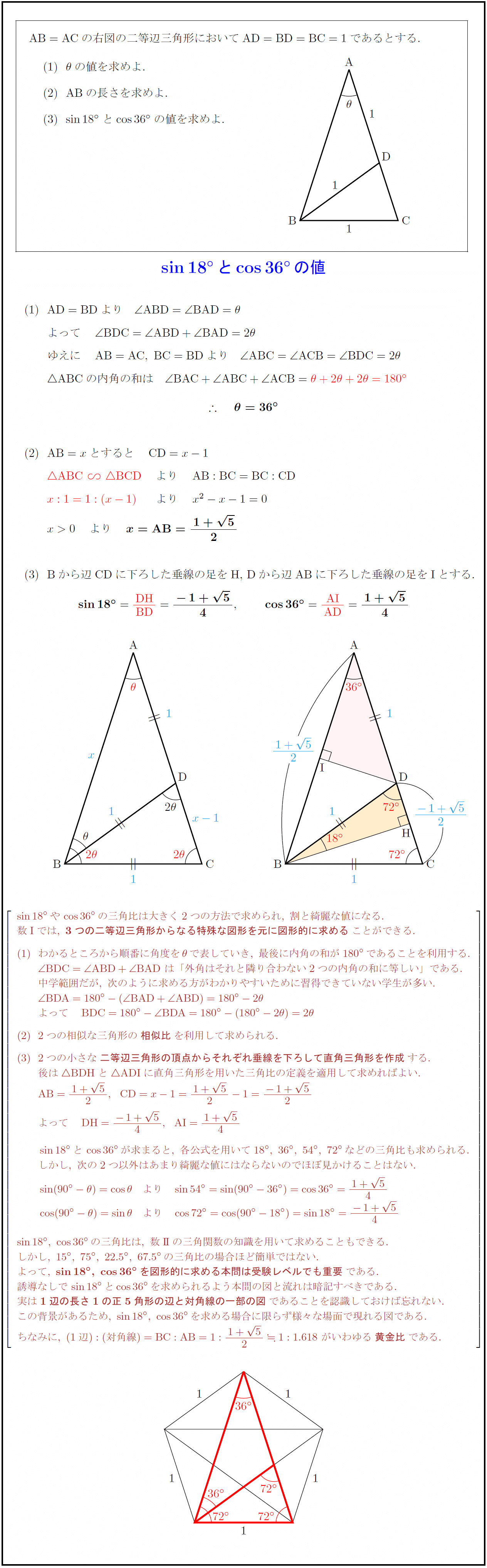



高校数学 Sin18 とcos36 の値 正五角形を利用した図形的解法 受験の月



第65問の解答
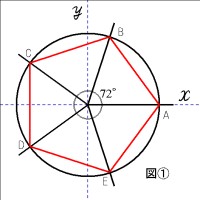



09年12月03日の記事 備忘録 楽天ブログ




多角形の内角の和の公式と外角の和を利用した角度の求め方
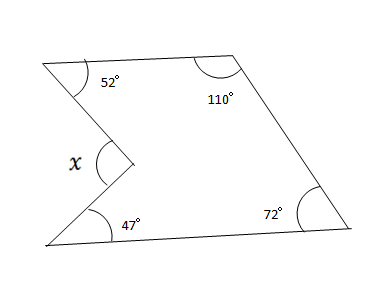



平行線と角度 8 ネット塾




正五角形というだけで 分かる角度は 名寄 算数数学教室より 算数 数学教室 数学



重なった正六角形と正五角形の角度 奈良学園登美ヶ丘中学 09年 早稲田中学 10年 算数解法の極意



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー




解決済み 多角形の角度指定 Adobe Support Community
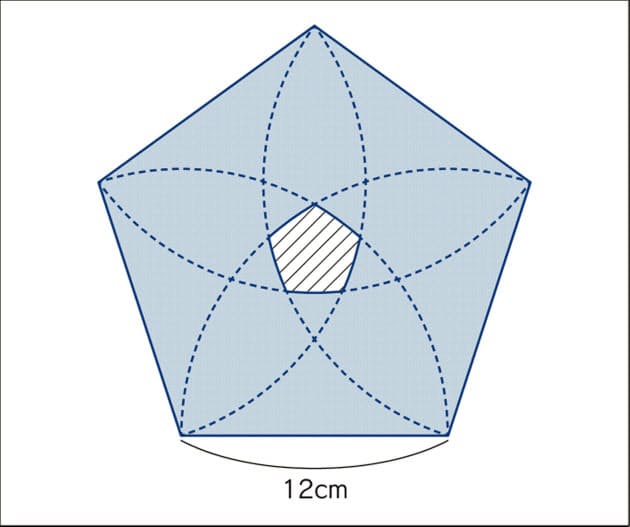



算数オリンピックに挑戦 第23回 Nikkei Style



1
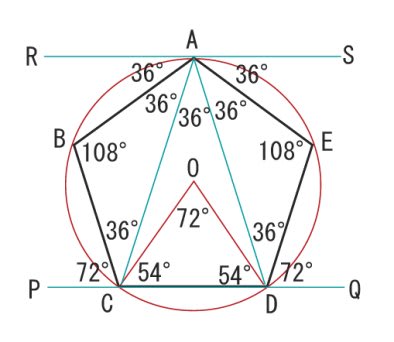



正五角形というだけで 分かる角度は 名寄 算数数学教室より



6年課題 算数 の問題解説1 課題の算数プリントの中で 間違いが多かった問題の解き方を考えましょう この問題は 五角形の5つの角の和の求め方を説明する問題です まず ひろとくんの考え方をわかりやすく考えてみましょう 問題の五角形の中



1
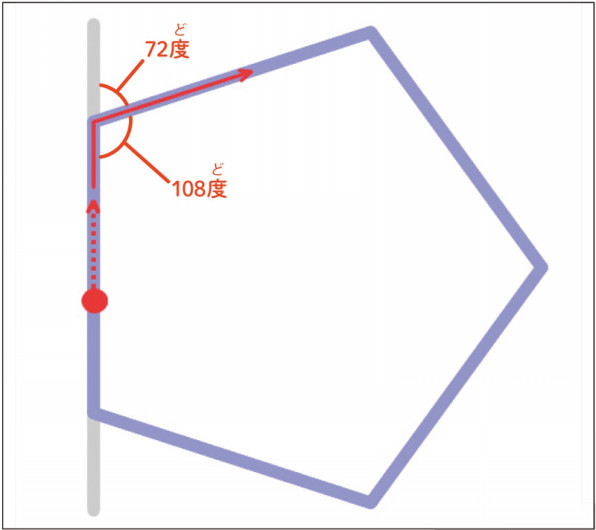



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




星型五角形の頂角の合計は 工坊



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみましたpart 2 日だまりのエクセルと蝉しぐれ



中二 五角形の内角の和の求め方 をアップ 久保塾 今治市の学習塾




多角形の内角の和 は何度なのか を説明します おかわりドリル



My Math Note




多角形の内角の和 外角の和の公式 数学fun




五角形と星形の相関図 Scratch Pythonプログラミング 作例



中学二年生の星形五角形の内角の和の求め方を教えてください 星 Yahoo 知恵袋
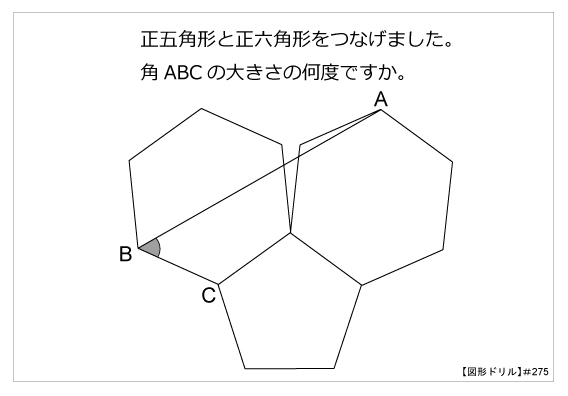



第275問 正五角形と正六角形 図形ドリル 第275問 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦




小学5年生 正多角形 算数 Active Learning 学院
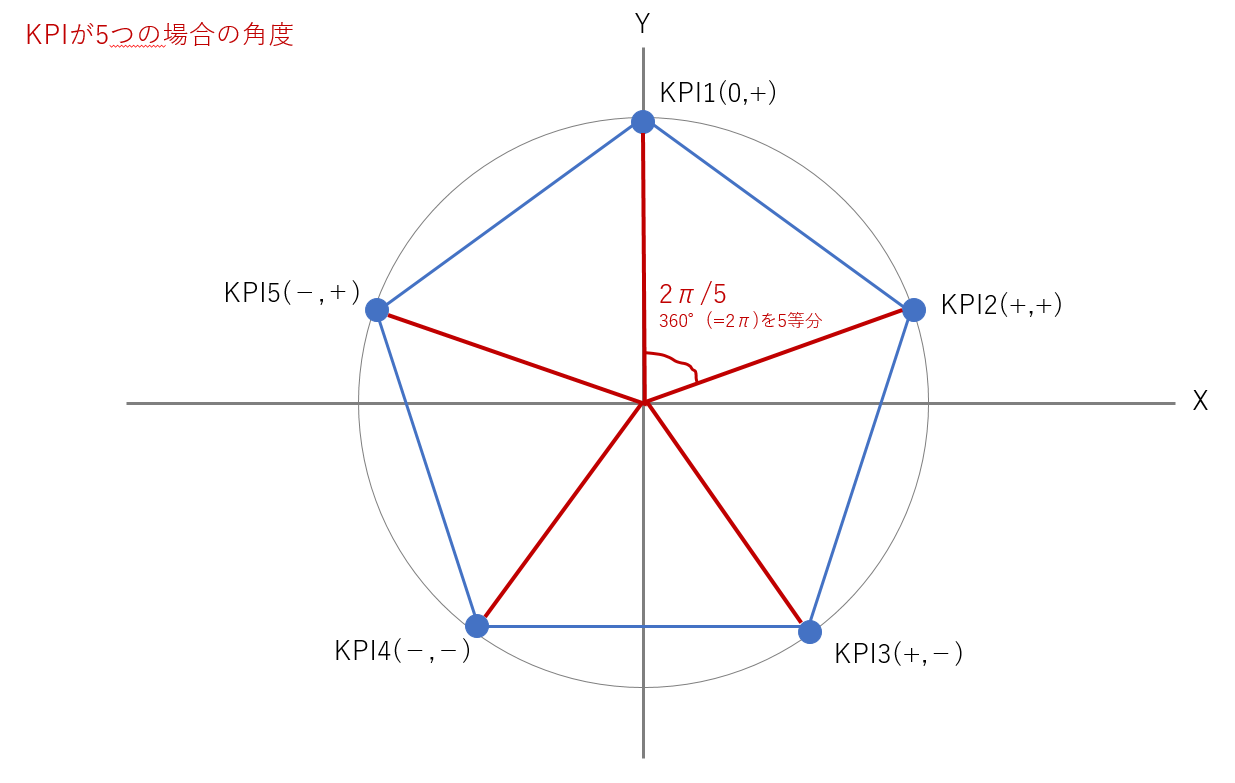



Tableauでレーダーチャートをつくってみた 応用編 Tabろぐ



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版



茗渓予備校 科目情報
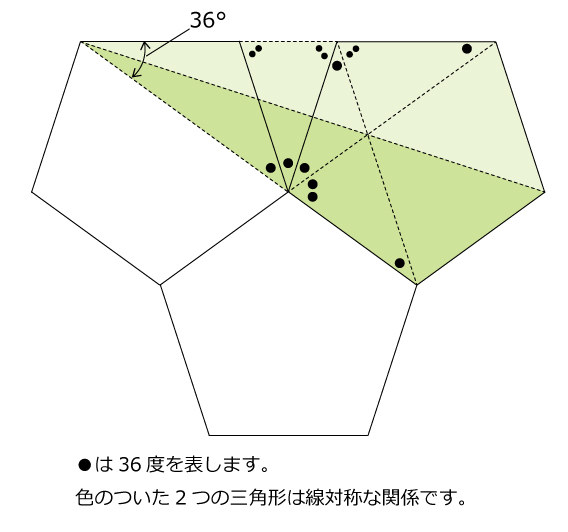



第314問 正五角形と角度 図形ドリル 第314問 正五角形と角度 算数星人のweb問題集 中学受験算数の問題に挑戦



正五角形と正三角形




隠された黄金比 対称性 ふしぎな魅力で人を惹きつける 図形 の秘密 柳谷 晃 ブルーバックス 講談社 2 2




すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント
コメント
コメントを投稿